弊社ではベイジアンネットワークの分析ツール BAYGLE / PLASMA を開発・販売しています。
ここではベイジアンネットワークをこれから使ってみようと思っている人を対象に、ベイジアンネットワークについて概説します。
1. ベイジアンネットワークとは?
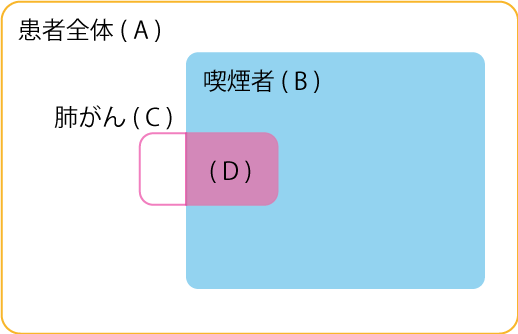
ベイジアンネットワークとはAI(機械学習)やデータマイニングで用いられる手法の一つで、事象間の因果関係を表現できるという特徴を持っています。例えば、図 1は病気の診断モデルで、次のような知識を表現しています。
- 喫煙が肺がんや気管支炎のリスクファクターとなっている。
- 結核または肺がんに罹患することによりレントゲン検査が陽性となるが、逆にレントゲン検査からは結核か肺がんかを区別することはできない。
- 気管支炎、結核または肺がんにより呼吸困難という症状がでる。
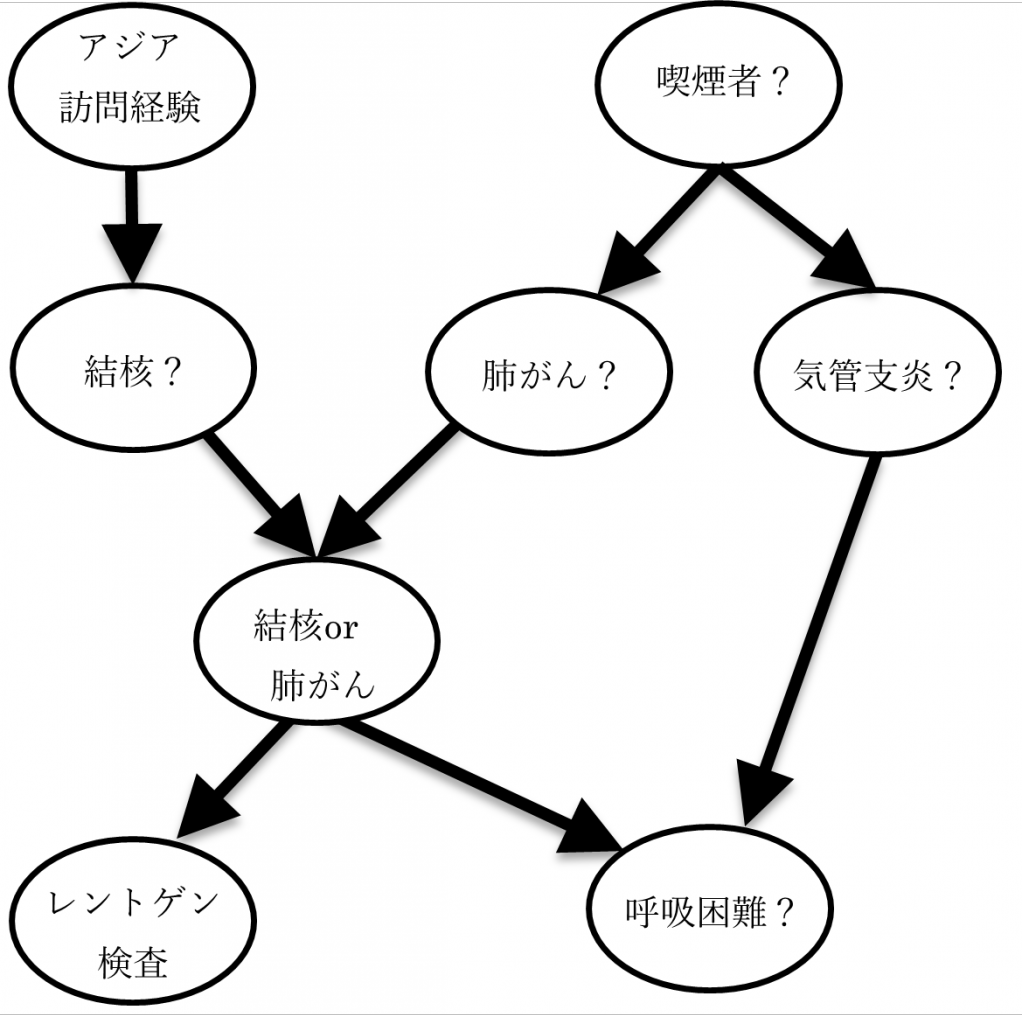
Lauritzen, Steffen L. and David J. Spiegelhalter (1988) “Local computations with probabilities on graphical structures and their application to expert systems” in Journal Royal Statistics Society B, 50(2), 157-194.
ベイジアンネットワークはこのような知識-事象間の因果関係-を表現するだけでなく、これを元に確率推論を実行することができます。
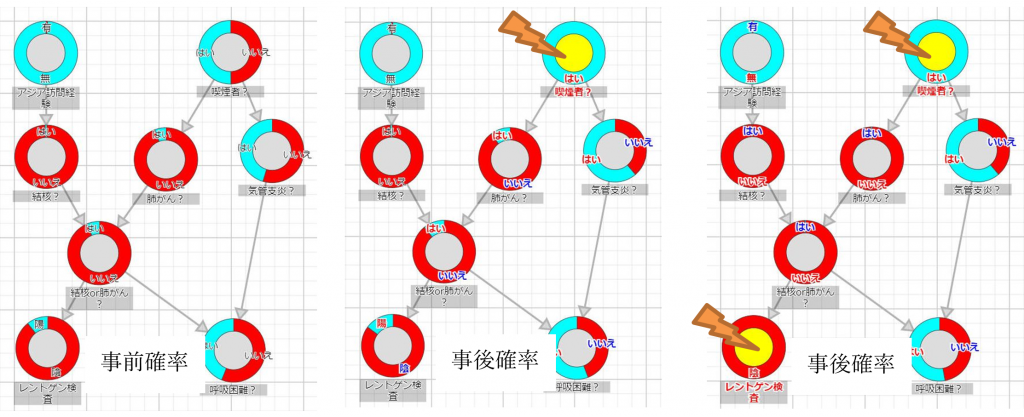
ベイジアンネットワークの楕円で表現しているものをノードと呼び、矢印をリンク(またはエッジ)と呼びます。このノードは実は確率変数で 図 2のように、それぞれ確率分布を持っています。何も情報がない状況での確率分布を事前確率と呼びます。ここで例えば、ある患者さんが喫煙者だと分かれば、その情報を入力すると「喫煙者?」を除く他の変数の確率分布が更新され、これが「喫煙者?=はい」の観測後の確率となっており、これを事後確率と呼びます。さらにレントゲン検査を行いその結果が陰性であれば、またその情報を入力すると、その他の確率変数の確率分布が更新されます。
ベイジアンネットワークの確率推論では、何から何を予測するといったことは決まっていません。得られた情報から、情報が得られてない確率変数の確率分布を更新するというシステムです。下図のような診断モデルであれば通常は問診結果、検査結果や症状から病気の確率を推論するのが通常の使い方ですが、逆に病気の方に情報を入力することで、どういう人がその病気になりやすいのか、またどういう症状が発生しやしいかといった知見を得ることもできます。
2. ベイジアンネットワークの定義
確率変数を頂点とする有向非循環グラフと、次の条件付き確率表を合わせてベイジアンネットワークと呼びます。
P(X | parents(X))チェストクリニックモデル(図 1)には次の8個の条件付き確率表がそのベイジアンネットワークの定義として含まれます。
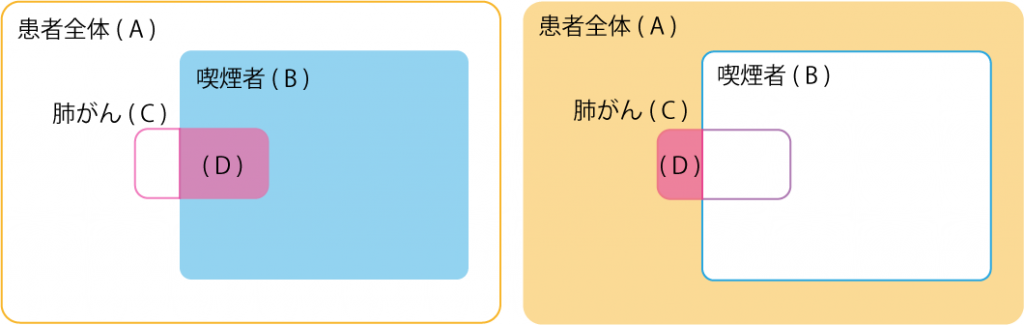
P(アジア訪問経験)、P(喫煙者?)、P(結核?|アジア訪問経験)、P(肺がん?|喫煙者?)、P(気管支炎?|喫煙者?)、P(結核or肺がん|結核?、肺がん?)、P(レントゲン検査|結核or肺がん)、P(呼吸困難|結核or肺がん、気管支炎?)条件付き確率表:P(肺がん?|喫煙者?)は喫煙者かどうかが分かっている場合の肺がんの確率です。P(肺がん?|喫煙者?=はい)はベン図(図 3左)で書くと、肺がん(C)と喫煙者(B)の共通部分をDとするとD/B となります。これと喫煙者でない場合(図 3右)も合わせて次表となります。
| 喫煙者 | |||
| いいえ | はい | ||
| 肺がん | いいえ | 0.990 | 0.898 |
| はい | 0.990 | 0.898 | |
喫煙していない人の「肺がん=はい」の確率が約1%なのに対して、喫煙している人の確率が約10%と高いという知識を表現しています。
ベイジアンネットワークはその矢印が確率的な依存関係を定性的に、また条件付き確率表が定量的に表現しています。グラフ構造も条件付き確率表も意味が明確で分かりやすいところがベイジアンネットワークの良いところです。このようにベイジアンネットワークは人が理解できますので、知識のみから構築することや、人の知識とデータを合わせてモデルを構築することができます。
3. 確率推論とは何をしているのか?
3.1. チェーンルール
ベイジアンネットワークは確率変数の同時確率を定義しています。P(肺がん?|喫煙者?)と書くとこれは条件付き確率で、P(肺がん?, 喫煙者?)と書くとこれは同時確率(結合確率とも呼ぶ)です。前者は喫煙者?の中で肺がん?である確率で、後者は喫煙者?でかつ肺がん?である確率です。ベン図では前者がD/Bで、後者がD/Aです。
ベイジアンネットワークの構造は、全確率変数の同時確率が次のように条件付き確率の積で書けることを表現しています。これをチェーンルールと呼びます。
P(X1,X2,…,Xn)=\Pi P(Xi|parents(Xi))\\Xi は ベイジアンネットワークの構成要素の確率変数
チェストクリニックモデルでは次のようになります。
P(ア, 喫, 肺, 結, 気,結or肺,レ,呼)= P(ア)P(喫)P(結|ア)P(肺|喫)P(気|喫)P(結or肺|結,肺)P(レ|結or肺)P(呼|結or肺,気)例えば全変数が互いに独立であればグラフ構造では矢印はなくなり、同時確率は次のように個々の確率分布の積となります。
P(ア, 喫, 肺, 結, 気,結or肺,レ,呼)= P(ア)P(喫)P(結)P(肺)P(気)P(結or肺)P(レ)P(呼)
同時分布が定義できると、ここから任意の状況での確率分布を計算することができるようになります。
3.2. 確率推論
ベイジアンネットワークは、情報を観測した後の確率(事後確率)を高速に計算するシステムです。先ほどの例(図 2)では同時分布
P(ア, 喫, 肺, 結, 気,結or肺,レ,呼)= P(ア)P(喫)P(結|ア)P(肺|ア)P(気|喫)P(結or肺|結,肺)P(レ|結or肺)P(呼|結or肺,気)から、P(肺がん?|喫煙者?=はい, レントゲン検査=陰性)を計算していました。これを計算するのに使うのは周辺化と乗法定理だけです。
周辺化:同時分布から不要な変数を取り除き必要な変数だけの確率分布を得る方法です。不要な変数の全ての状態で確率値を合算することで得られます。簡単のため二変数の場合で考えます。同時分布 P(喫煙者?, 肺がん)から P(肺がん)の確率分布を知りたいには、次のように喫煙者?の全ての状態で和を取れば良いのです。
P(肺がん)=\displaystyle\sum_{喫煙者} P(喫煙者,肺がん)\\=P(喫煙者=はい,肺がん)+P(喫煙者=いいえ,肺がん)乗法定理:同時確率は次のように条件付き確率の積に分解することができます。
P(喫煙者 ,肺がん)=P(喫煙者|肺がん)P(肺がん)=P(肺がん|喫煙者)P(喫煙者)
この式より、条件付き確率が次のように計算できます。
P(喫煙者\vert肺がん)=\cfrac{P(喫煙者 ,肺がん)}{P(肺がん) }ではP(肺がん?|喫煙者?=はい, レントゲン検査=陰性)を計算してみましょう。まず対象となる3変数の同時分布を計算します。
乗法定理より
P(喫煙者 | 肺がん,レントゲン検査)=\cfrac{P(喫煙者 ,肺がん,レントゲン検査)}{P(肺がん,レントゲン検査) }周辺化より
P(肺|喫,レ)=\cfrac{\displaystyle\sum_{ア,結,気,肺or結,呼}P(\underlineア,喫,肺,\underline結,\underline気,\underline{肺or結},レ,\underline呼)}{\displaystyle\sum_{ア,肺,結,気,肺or結,呼}P(\underlineア,喫,\underline肺,\underline結,\underline気,\underline{肺or結},レ,\underline呼)}\\=\cfrac{\displaystyle\sum_{ア,結,気,肺or結,呼}P( 喫,肺,レ)}{\displaystyle\sum_{ア,肺,結,気,肺or結,呼}P( 喫,レ)}これを単純に計算すれば推論結果が得られるのですが、変数の数が多くなると和を取るべき状態の組み合わせがあっという間に膨大な量となり計算が困難になります。ここで条件付独立性を考慮することで和を取る組み合わせの数を減らすことができ、効率良く計算を行うことが可能となります。このように周辺化をベースにして厳密にかつ高速に確率推論を行うアルゴリズムにBelief Propagation Algorithmがあります。また正規分布から正規乱数を生成するのと同様に、ベイジアンネットワークが定義する同時確率から、それに従ったデータを生成することができます。そのデータを集計することで事後確率を計算する方法をサンプリング法と呼びます。
4. ベイジアンネットワークを作る
ベイジアンネットワークは人が理解できますので完全に人の知識からデータ無しでモデルを作ることもできますが、ここではデータからベイジアンネットワークを構築する方法について簡単に説明します。データから統計モデルを構築することを「学習」と呼びますが、ベイジアンネットワークではそのグラフ構造をデータから探索する「構造学習」と、条件付き確率表をデータから推定する「パラメータ学習」の二つの学習があります。
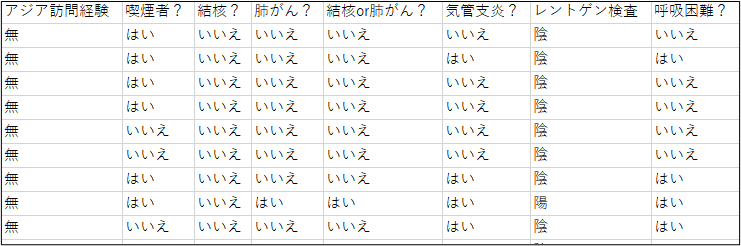
例えば、チェストクリニックモデルは図 4のようなデータから構築しています。また構造学習の際には、その探索範囲を与えることで人の知識を反映することができます。ある変数に対する親候補、必ず親にする変数、絶対親にしない変数を指定することができます。
また構造学習のアルゴリズムにはスコアベースのアルゴリズムと制約ベースのアルゴリズムがあります。
スコアベース:スコアベースというのは、ベイジアンネットワークの構造を評価する評価関数がありその値が一番良くなる構造を探索する方法です。これは組み合わせ最適化問題となり現在のコンピュータを持ってしても解くことは困難なため、欲張り法や局所探索法などを用いて近似解を求めます。また評価関数には情報量規準と呼ばれる指標を用います。
制約ベース:ベイジアンネットワークは変数間の確率的な依存関係を表現しています。変数間に確率的な依存関係があるのか、ない(独立)のかはデータからある程度調べることができますので、これを使ってデータから構造の復元を試みる方法です。
5. ベイジアンネットワークを使う
ここではベイジアンネットワークのユースケースをご紹介します。実際の実例をベースにしていますが、ここには書けないことも多く、一部、フィクションを含めイメージしやすいように書いています。
5.1. POSデータの分析
毎日溜まり続けるPOSデータ、しかしPOSデータには顧客IDと買われた商品の情報しかありません。もしその顧客の属性、嗜好やライフスタイルなどの情報が分かれば、マーケティング、販促などに役立てることができます。
そこで顧客の一部にライフスタイル等の知りたい情報をアンケートで収集し、そのアンケートと購買履歴を合わせてベイジアンネットワークを構築します。そうすると、アンケートを取得していない人に対しても、その購買履歴からライフスタイル等の知りたい情報を予測することができるようになります。
また、人のライフスタイルは時間がたてば変化します。その変化により購買行動が変化すれば、同じ人でも昔と今ではライフスタイルの予測結果が変わってきますので、日々たまり続けるPOSデータからライフスタイルの変化をとらえることができるようになります。
5.2. アンケート分析
アンケートデータから購買行動モデルをベイジアンネットワークで表現することにより、一つのモデルで様々な状況をシミュレーションできるようになります。
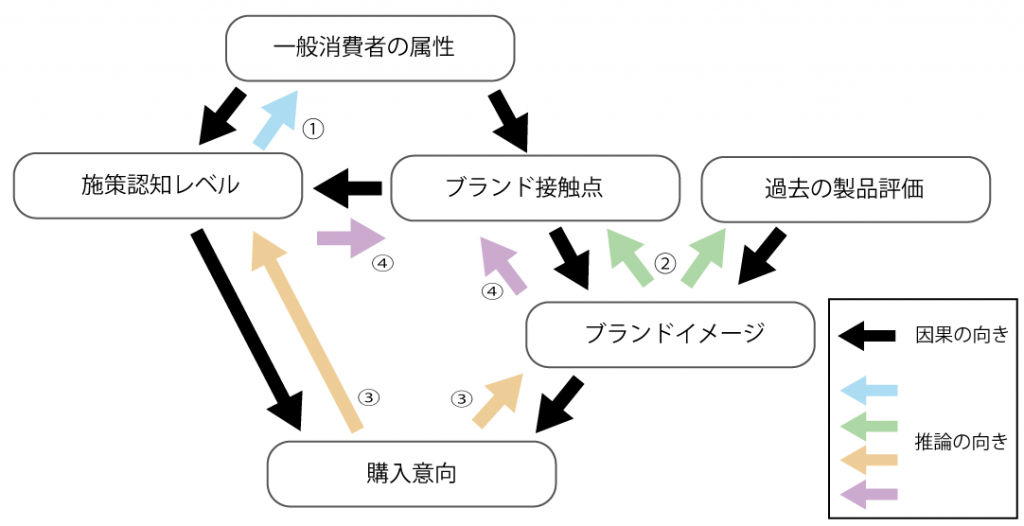
①「一般消費者がどんな施策を認識しているか?」が知りたい場合には
→ 属性から施策を推論
②「ブランドイメージに寄与する要因は?」が知りたい場合には
→ ブランドイメージからブランド接触点、過去の製品評価を逆向きに推論
③「購入に寄与する要因はブランド?施策?」が知りたい場合には
→購入意向かあら施策の認知レベル、ブランドイメージを逆向きに推論
④「購入に寄与する接触点は?」が知りたい場合には
→ さらに施策に認知レベル、ブランドイメージからブランド接触点を逆向きに推論
5.3. マッチングシステムへの応用
保育士に就職先(保育園)を紹介する際に、性格診断を双方に実施し、相性を評価することで定着率の向上を実現しており、この知見をAI(ベイジアンネットワーク)で表現し誰でも簡単にできるようにしたいというプロジェクトです。
本件では過去のデータが 200 件ほどしかなかったためデータから構造を決めることは難しく、人の知見を取り入れることで、目的に沿ったモデルが構築しました。担当者の知見を元に構造を決め、条件付き確率表のみをデータから計算するという方法を採用しました。
ミスマッチを無くし保育士の定着率を上げることが目標ですので、勤続年数(1 年以上勤務)を目的変数としたモデルとしました。説明変数には性格診断を保育園側と保育士側実施して頂き、その相性を組み込んでいます。保育業界では諸所の勤務条件が満たされていることが前提となりますが、保育園と保育士の相性が大きく定着率に影響し、また退職経験がありその理由が人間関係の場合にさらにその影響が大きくなるという知見をベイジアンネットワークの構造として表現しました。
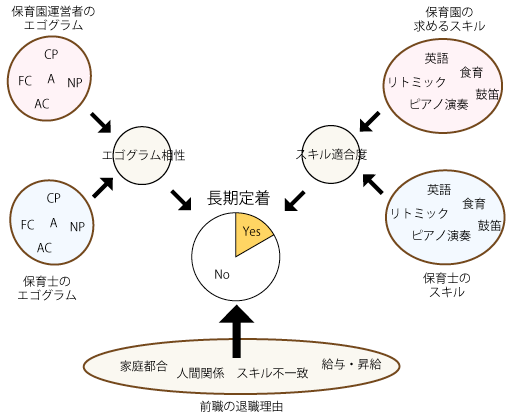
ベイジアンネットワークは人の知識とデータを合わせてモデルを構築することで、少ないデータでもある程度の精度をもったモデルを構築することができます。これを初期モデルとしてシステムをリリースし、利用履歴がたまればこれを学習データとしてモデルを更新することで精度を上げていきます。
5.4. eラーニングへの応用
ベイジアンネットワークは情報が観測された変数から、情報が観測されていない残りの全変数の事後分布を高速に計算するシステムです。この特徴を生かした事例になります。
レコメンド
各教科の学習単位をここでは単元と呼ぶこととします。単元間には依存関係があり、例えば数学では一次関数と二次関数という単元があって一次関数が理解できていないと二次関数を理解できません。
そのような関係を全てつなぎ合わせると、数学全体の単元間の依存関係を表現したベイジアンネットワークができあがります。
そのベイジアンネットワークに学習者の現在の履修状況を反映することで、こことここが理解できているのならこの単元も理解できているのではないか、こことここを間違えているのならここが理解できていないのではといったことが確率推論により推定できるようになります。
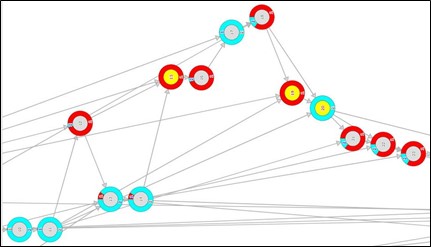
図 5では中心が黄色のノードが履修済みの単元、周辺に赤色が多いノードが理解できていないと推定された単元、周辺に青色が多いノードが理解できていると推定された単元です。さらに未履修の単元が仮に理解できたときに、他の未履修の単元の状態がどのように変化するのかということも分かるようになります。このような情報を元にして次のどこへ進むのか、またはどこに戻るのかをレコメンドします。